Date
Monday, September 10th, to Thursday, September 13th
Location
Organizers
Simon Schmidt und Andrea Thevis (Saarbrücken)
Title
Game Theory
Participants
| Name |
|---|
| Daniel Gromada |
| Benedikt Hewer |
| Pascal Kattler |
| Felix Leid |
| Laura Maaßen |
| Emil Rotilio |
| Simon Schmidt |
| Ricardo Schnur |
| Christian Steinhart |
| Andrea Thevis |
| Andreas Widenka |
| Sheng Yin |
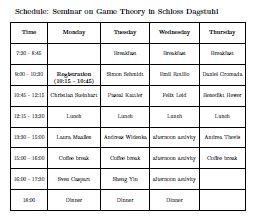
Schedule
Description of the talks
| Title | Description | Literature | Referee |
|---|---|---|---|
| TAKE-AWAY-GAMES AND THE GAME OF NIM | This talk introduces basic definitions and concepts which are important for other talks (e.g., perfect information, combinatorial, impartial, partizan game). We then study different types of games: Take-Away-Games can be analyzed with the help of P- and N-positions and backward induction. (Also mention subtraction games which are a generalization of Take-Away-Games.) The Nim-sumis used to study the Game of Nim. | Introduction, Chapter I Section 1 and 2 of [Fer] | Christian Steinhart |
| GRAPH GAMES AND SUMS OF COMBINATORIAL GAMES | In this talk we define directed graphs and use themto describe and study combinatorial games. We then introduce the Spargue-Grundy function. This function can be used to analyze combinatorial game. (show this on an example) In the second part of the talk, we define the sum of graph games. We discuss the Spargue- Grundy theorem and its applications. | Chapter I Section 3 and 4 of [Fer] | Laura Maassen |
| COIN TURNING GAMES | The goal of this talk is to introduce and study Coin Turning Games. | Chapter I Section 5 of [Fer] | |
| GREEN HACKENBUSH | In this talk we study the game Green Hackenbush (see [Fer]). For this, we use concepts introduced in the previous talks, e.g. the Spargue-Grundy function. If time permits, we discuss a generalization called Blue-Red Hackenbush (see [BCG]). | Chapter I Section 6 of [Fer] and [BCG] | Sven Caspart |
| STRATEGIC FORM AND MATRIX GAMES | In this talk, we introduce the strategic form of a two-person zero-sum game and state theMinimax Theorem, which will also appear in other talks. Finite two-person zero-sum games are also called matrix games and in the second part of this talk we discuss 2x2, 2xn and mx2 matrix games as well as Latin square games. | Chapter II Section 1 and 2 of [Fer] | Simon Schmidt |
| PRINCIPLE OF INDIFFERENCE | We first state the Equilibrium Theorem in this talk, which leads us to the Principle of Indifference. We use this principle to solve games like the diagonal, triangular and symmetric games. Then we introduce the concept of Invariance and consider Colonel Blotto games (a class of tactical military games) as example. | Chapter II Section 3 of [Fer] | Pascal Kattler |
| SOLVING FINITE GAMES | This talk introduces the Bayes strategy, also called best response. We express theMinimax Theorem more simple and prove it by reducing it to a linear programming problem. Then we describe the PivotMethod for solving games and give an example. | Chapter II Section 4 of [Fer] | Andreas Widenka |
| EXTENSIVE FORM | In this talk we introduce the extensive form of a two-person zero-sum game, modelled by a directed graph. We show that one can represent strategic formgames in extensive formand reduce a game in extensive formto a game in strategic form. We look at games of perfect information which are games in extensive formand behavioral strategies which are useful for such games. | Chapter II Section 5 of [Fer] | Sheng Yin |
| RECURSIVE AND STOCHASTIC GAMES | We start with defining matrix gameswith games as components and look at Decomposition of such games. Then we discuss multistage games and define recursive games. There are \epsilon-optimal strategies for such games. The second part of the talk concerns stochastic games. We define those games and look at the Shapley iteration which approximates the solution. | Chapter II Section 6 of [Fer] | Emil Rotilio |
| INFINITE GAMES | The first part of this talk deals with semi-finite games, where we state theMinimax theorem and look at solutions of such games. After that, we discuss continuous games, concave and convex games. If time permits, we compare two uniform[0,1] pokermodels. | Chapter II Section 7 of [Fer] | Felix Leid |
| BIMATRIX GAMES AND NONCOOPERATIVE GAMES | This talk introduces the strategic form and the extensive form of two-person general-sumgames. Bimatrix games are finite two-person general-sum games. The second part of this talk deals with noncooperative games. We will see that every finite n-person game has at least one strategic equilibrium, also known as Nash equilibrium. | Chapter III Section 1 and 2 of [Fer] | Daniel Gromada |
| MODELS OF DUOPOLY | In this talk, we look at different models of Duopoly (two sellers/firms in one market), namely the Cournotmodel, the Bertrand model and the Stackelberg model. | Chapter III Section 3 of [Fer] | Benedikt Hewer |
| COOPERATIVE GAMES | This talk concerns cooperative games, where we distiguish between cooperative games with transferable utility and those with non-transferable utility. The latter can be approached through the Nash Bargaining Model. Another approach is the Lambda-Transfer due to Shapley. | Chapter III Section 4 of [Fer] | Andrea Thevis |
| GAMES IN COALITION FORM | The goal of this talk is to analyze in which situations different players should forma coalition and how to distribute the profit. After giving introducing formal definitions of games in coalition form and characteristic functions, we explain how a game in coalition form can be transformed into strategic form and vice versa. We then discuss the distribution of the profit won while playing a game in a coalition. Finally, we discuss the power of individual players in a coalition. | Chapter IV Section 1 to 3 of [Fer] |
Literature
[Fer] Game Theory by Thomas S. Ferguson
[BCG] Winning Ways for your Mathematical Plays by E.R. Berlekamp, J.H. Conway, and R.K. Guy